Paired T Test Example
The truth is that doing a paired t test is not as difficult as it may seem when you first look at it. Nevertheless, a paired t test example is always a good way to learn exactly what you need to do.
One of the things that you need to have in mind os that a paired t test is used to compare the means of two populations.
Use the top stats calculators.
The paired t test is very used in many different areas. You can use it to compare different health treatments, to analyze the results of a diagnostic test before and after a specific module, among so many others.

Before we actually show you the paired t test example, let’s see how you need to proceed.
Let’s say that you have a sample of n students. They had to do a diagnostic test before module A and another one after completing it. Our goal is to determine the importance of teaching in the student’ skills and knowledge, evaluated with their scores.
Let’s also consider that:
x – represents the diagnostic test score before Module A
y – represents the diagnostic test score after Module A
In order to start testing the null hypothesis, which is the mean difference is zero, here are the steps you need to take:
Step #1: Calculate the difference between the two observations, before and after the diagnostic test, on each pair:
d = y – x
Learn more about the unpaired t test.
Step #2: Determine the mean difference
Step #3: Determine the standard deviation of the differences. Then, you will need to use this value to calculate the standard error of the mean difference:
![]()
Step #4: Determine the t-statistic, by using the following formula:
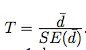
Please remember that you are testing the null hypothesis. Therefore you need to use the t-distribution with n-1 degrees of freedom.
Step #5: Compare your T value with the tn-1 value that you can check on the t-distribution tables.
Now, let’s check a practical paired t test example:
Let’s say that we are assuming that we want to measure the results of teaching on students as well and that we already know their scores before and after the Module A was taught. Let’s also consider that we are considering a sample of 20 students. So, n = 20.
Here are the scores that the students had:
| Student | Pre-Module Score | Post-Module Score | Difference |
|---|---|---|---|
| 1 | 18 | 22 | +4 |
| 2 | 21 | 25 | +4 |
| 3 | 16 | 17 | +1 |
| 4 | 22 | 24 | +2 |
| 5 | 19 | 16 | -3 |
| 6 | 24 | 29 | +5 |
| 7 | 17 | 20 | +3 |
| 8 | 21 | 23 | +2 |
| 9 | 23 | 19 | -4 |
| 10 | 18 | 20 | +2 |
| 11 | 14 | 15 | +1 |
| 12 | 16 | 15 | -1 |
| 13 | 16 | 18 | +2 |
| 14 | 19 | 26 | +7 |
| 15 | 18 | 18 | 0 |
| 16 | 20 | 24 | +4 |
| 17 | 12 | 18 | +6 |
| 18 | 22 | 25 | +3 |
| 19 | 15 | 19 | +4 |
| 20 | 17 | 16 | -1 |
In the last column, you can already see the calculations of the differences of the scores for each student. So, all you need to do know is to determine the mean difference, using the formula we provided above.
We can then say that the mean difference is 2.05.
So, by using the values and replacing them in the standard deviation of the differences formula also provided above, you will get:
Sd = 2.837
Now, it’s time to determine the standard error of the mean:
SE(d) = Sd / √n = 2.837 / √20 = 0.634
Discover the top intro statistics books.
Finally, you will need to perform the t-statistic:
t = 2.05 / 1.634 = 3.231
Please notice that this is the t-statistic calculated for 19 degrees of freedom.
So, by looking at the tables, you can see that you will get a p = 0.004.
With this result, we can say that module A does lead to improvement in the students’ knowledge and skills. In fact, there is even a strong evidence of that.