Count Variables Vs Continuous Variables: Understanding The Differences

When you are looking at data statistics, there are many relevant concepts. And the reality is that one of the most important things that you need to realize is that the analysis needs to be appropriate for the scale of measurement of the variable. Notice that the focus of these decisions about scale needs to focus on levels of measurement that can be nominal, ordinal, ration, and interval.  

One of the things that you should keep in mind about these levels of measurement is the fact that they tell you about the amount of information in the variable itself. However, there are other ways to establish the difference between scales. 

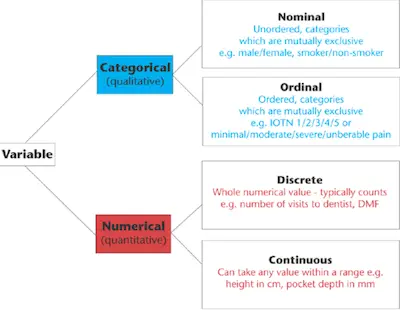
If you take a closer look at ratio-level variables, for example, you can find two different types: discrete and continuous. While discrete variables only take integers, continuous variables take on any value on a number line. In case you are wondering why this matters in statistics, the reality is that you measure the probabilities in a different way depending on if they are discrete or continuous distributions. 

The probability of each value of a discrete random variable is described through a probability distribution. At its simplest, this is a list of all the values in the set and the probability of each value occurring.

Discover how to calculate t value.

However, you need to know that the probabilities of many discrete random variables follow patterns that can be described with a mathematical function. This function is called a probability mass function.

As you can imagine, there are numerous discrete probability distributions including Bernoulli, binomial, hypergeometric, discrete uniform, and Poisson. There are explicit criteria that determine which probability distribution is appropriate for a specific discrete random variable.

Count data are a good example. A count variable is discrete because it consists of non-negative integers. Even so, there is not one specific probability distribution that fits all count data sets.

Looking for a t value calculator online?

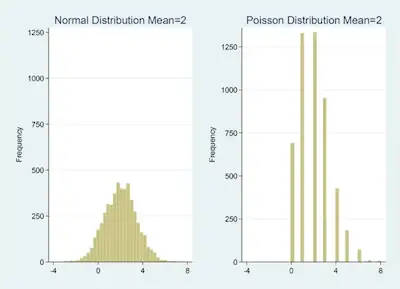
The Poisson distribution often fits count data. It fits well when the mean of the variable is equal to its variance. So how do you determine that?

All you need to do is to run a summary of your variable in your statistical software package and then compare the mean to the variance. If the standard deviation is listed instead of the variance, just square the standard deviation. If they are almost equal, then that’s a good sign.

But many count variables fail these tests.

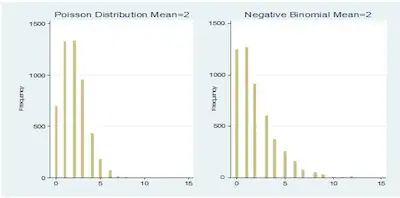
Below are two graphs generated with Poisson and negative binomial probability distribution functions. Each has 5,000 observations. The mean of the Poisson data is 2, the variance is 1.99, and the range is from 0 to 8. The mean of the negative binomial data is 2, the variance is 4.16, and the range is from 0 to 15.

The negative binomial distribution contains an extra parameter that allows the variance to be greater than the mean. If you tried to fit a data set with that mean and variance to a Poisson distribution, it would be considered overdispersed — not a good fit.

Check out our quick t student calculator.

The Normal Distribution

If the mean of a Poisson or negative binomial variable is high enough, it will be symmetric and bell-shaped. It will look like a normal distribution, except for one key distinction – normal variables are truly continuous, not discrete. This means that they can take on any possible value.

As a result, there are an infinite number of values (2.30546 is a different value than 2.30547). So, it makes no sense to calculate the probability that X is any exact value in a continuous variable. That probability is infinitesimal, a value approaching zero.

With continuous variables, the probability of a value falling within a range is calculated instead. For example, there is a 95% probability that a value from a normal distribution will fall within 1.96 standard deviations of the mean of that distribution.

To show you the difference, I created a set of 5,000 random values from a normal distribution with a mean and variance of 2. The range of the data is -2.512433 to 7.461702. Included next to its graph is the graph of the Poisson variable with a mean and variance of 2.