Covariance Calculator (from a Correlation Coefficient)

Use this free calculator to compute the covariance between two variables X and Y given correlation coefficient (Pearson’s) and standard deviations.

Please input values in the required fields and click CALCULATE.

Correlation between X and Y:

Standard deviation for X:

Standard deviation for Y:

What Is Covariance

In the world of statistics, covariance is a very important concept that you should always keep in mind. Simply put, covariance is a measure of how much two random variables can vary together. In case you notice, the covariance concept is very similar to the variance concept. However, the variance tells you how a single variable varies while covariance tells you how two variables vary together. Make sure to use our covariance calculator.

The Covariance Formula

When you want to determine the covariance, all you need to do is to use the following formula:

Cov(X,Y) = Σ E((X-μ)E(Y-ν)) / n-1

Where,

X is a random variable

E(X) = μ is the expected value (the mean) of the random variable X and

E(Y) = ν is the expected value (the mean) of the random variable Y

n = the number of items in the data set

Practical Example

Let’s say that you want to calculate the covariance of the following data set:

x: 2.1, 2.5, 3.6, 4.0 (mean = 3.1)

y: 8, 10, 12, 14 (mean = 11)

As we told you, all you need to do is to use the covariance formula. So,

Cov(X,Y) = ΣE((X-μ)(Y-ν)) / n-1

Cov(X,Y) = (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)

Cov(X,Y) = (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3

Cov(X,Y) = 3 + 0.6 + .5 + 2.7 / 3

Cov(X,Y) = 6.8/3

Cov(X,Y) = 2.267

Since you got a positive covariance, this means that the variables are positively related. Confirm your results in our free covariance calculator located at the top of this page.

Note:

If you check the denominator of the formula, you have the degrees of confidence. Since in this example we had more than 2 terms we used the formula n – 1. However, when you are just trying to determine the covariance of two random variables, then you will need to divide the formula by n only.

Interpreting The Covariance

As we stated above, since we had a positive covariance, we could state that there is a positive relationship between the variables or that they are positively related. Make sure to try out our calculate covariance from correlation.

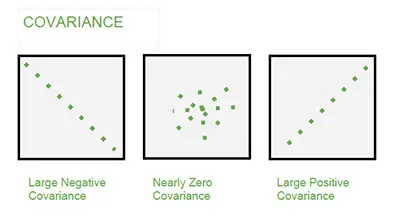
As a rule of thumb, a large covariance means that there may be a strong relationship between variables. Nevertheless, you need to keep in mind that you can’t compare variances over data sets that have different scales. Just think about comparing two sets of variables where one set is expressed in inches and the other one in pounds.

Due to this problem with the interpretation of covariance results, a far better approach is to use the correlation coefficent. So, you should use the following formula instead:

Corr(X,Y) = Cov(X,Y) / σXσY

In case you prefer (and we advise you that you should), you can always confirm your results in our calculate covariance from correlation.

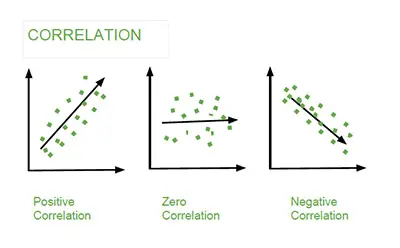
Why Should You Use The Correlation Coefficient?

The truth is that we already stated that using the correlation coefficient is a far better approach than to use the covariance when you want to determine the strength of the relationship between variables. But here are the explanations:

While the correlation doesn’t have units, covariance always has units
Covariance can use almost any number while a correlation can only take a number between -1 and +1
Correlation isn’t affected by the changes in the center (mean) or with the scale of variables
Since it has some numerical limitations, correlation tends to be more useful when you need to determine how strong a relationship is between the two variables.