Standard Error Calculator
This free online calculator will return the standard error of the mean given a set of observations (values).
Standard error (SE) of the mean represents the standard deviation (SD) of a sample mean estimate of the population mean. This calculation assumes statistical independence of the sample observations.
Please enter a set of numbers in the field (you can copy and paste using ctrl+v & ctrl+c) and click CALCULATE.
When you are studying statistics, you may have the need to determine the standard error. So, you’ll be glad to know that we created our own free standard error calculator that you can use anytime you need it. However, before we tell you a bit more about our standard error calculator, we understand that it is important that you know a bit more about the standard error but also about the standard deviation. So, let’s start with the latter.
What Is The Standard Deviation?
Simply put, the standard deviation tells you how your data is spread out. So, we can say that this is a measure that shows you how far each value you observed is from the mean.
It is worth to point out that in any distribution, around 95% of values will be within 2 standard deviations of the mean.
Discover how to find a confidence interval.
How To Calculate The Standard Deviation?
Notice that while you need to know how to calculate the standard deviation by hand in your statistics class, this is hardly ever done manually. The truth is that in most cases, you will have too many numbers and it will be easier to use a calculator, for example.
Understanding the normality tests for statistical analysis.
Nevertheless, you should keep in mind that when you want to calculate the standard deviation, you will need to use the following formula:
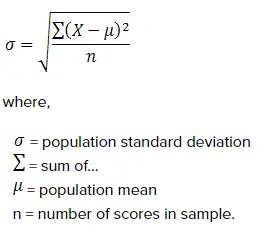
So, in order to calculate the standard deviation manually, you would need to:
- For each value, find its distance to the mean
- For each value, find the square of this distance
- Find the sum of these squared values
- Divide the sum by the number of values in the data set
- Find the square root of this
What Is The Standard Error?
When you hear someone referring to the standard error, this means they are referring to the standard deviation of multiple sample statistics like the mean or median. For example, when you hear someone mentioning “the standard error of the mean”, then you know this person is referring to the standard deviation of the distribution of sample means taken from a population.
Notice that the smaller the standard error, the more representative the sample is of the overall population.
Discover everything ou need to know about normal distribution.
The Relationship Between Standard Deviation And Standard Error
In case you are wondering why we started by defining the standard deviation, you are about to find out. The truth is that for any given sample size, the standard error is always equal to the standard deviation divided by the square root of the sample size.
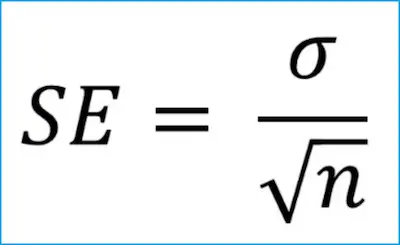
Notice that the standard error is inversely proportional to the sample size. So, ultimately, we can then state that the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
Bottom Line
As you can see, it would be very complicated to calculate the standard error and even the standard deviation manually. While you need to understand the process and know the formulas, you should use our standard error calculator to determine the standard error. After all, it’s incredibly easy to use it since you just need to add your set of numbers separated by comma.