Understanding Inferential Statistics

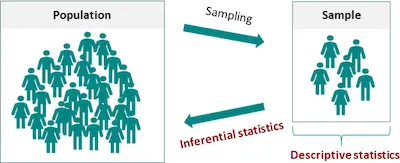
As you probably already know, inferential statistics is one of the two types of statistical analysis. Ultimately, it allows you to reach conclusions that go beyond the immediate data alone. To give you a simple example, inferential statistics allows you to infer from the sample data what the population may think. But this is not the only thing that it does.

Discover everything you need to know about statistics.

The reality is that inferential statistics also allows you to make judgments about the probability that an observed difference between groups is either dependable or one that may simply have happened by chance in this study. 

So, if you are trying to discover what is inferential statistics, then we can state that you use inferential statistics to make inferences from your data to more general conditions. 

Understanding Inferential Statistics

While there are many different inferential tests that you can perform, one of the simplest is when you want to compare the average performance of two groups on a single measure to see if there is a difference. For example, you may want to determine whether seventh-grade boys and girls differ in English test scores or whether a program group differs on the outcome measure from a control group. 

So, when you want to make this comparison or a similar comparison between two groups, you need to use the t-test for differences between groups. 

Understanding the difference between association and correlation.

Notice that most of the major inferential statistics come from a general family of statistical models that are often called as General Linear Model. So, besides the t test, it also includes Analysis of Variance (ANOVA), Analysis of Covariance (ANCOVA), regression analysis, and many of the multivariate methods like factor analysis, multidimensional scaling, cluster analysis, discriminant function analysis, among others. 

Since the General Linear Model is very important, when you are studying statistics it is ideal to become familiar with these concepts. Notice that while we have only mentioned a simple example of a t test that you should conduct to make the comparison above, the reality is that as you get familiar with the idea of the linear model, you will be prepared for more complex analysis. 

Using The Inferential Data Analysis

One of the main points that you should keep in mind when studying inferential analysis is to understand how groups are compared. And this is embodied in the notion of the “dummy” variable. 

Notice that by “dummy” variables we don’t mean that they aren’t smart or anything like this. The reality is that this is the name that we have to work with.

Simply put, a dummy variable is just a variable that uses discrete numbers, usually 0 and 1, to represent different groups in your study. So, you can easily understand that dummy variables are a simple idea that allows some complicated things to happen. 

For example, let’s say that you are running a model and that you want to include a simple dummy variable. When this happens, you can model two different lines – one for each treatment group – with a single equation. 

These are the major advantages and pitfalls of using the z score.

Factors That Influence Statistical Significance

When you run the different inferential tests, there are different factors that you need to take into account since they influence statistical significance. These include:

#1: The Sample Size:

The larger the sample, the less likely that an observed difference is due to sampling errors. So, you can then state that when you are dealing with a large sample, you are more likely to reject the null hypothesis than when the sample is small. However, it is also important to make it clear that you may have a sample that is so large that the statistics determine a significant difference which is so small they are meaningless. 

#2: The Size Of The Difference Between Means:

The larger the difference, the less likely that the difference is due to sampling errors. So, you can then conclude that when you have a large difference between the means, the more likely it will be to reject the null hypothesis. 

#3: The Amount Of Variation In The Population:

When a population varies a lot (is heterogeneous), there is more potential for sampling error. So, when you have only a slight variation, the more likely it will be to reject the null hypothesis. 

Error In Statistical Testing

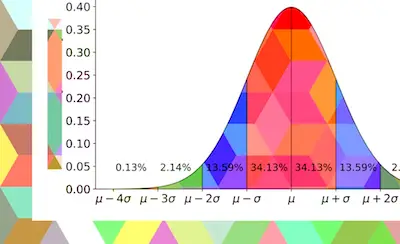
Notice that in most cases, the level of significance or alpha is set at the 0.05 level. So, in this case, the null hypothesis is rejected if the p value (that you get from a table) that results from the calculations from the data is less than or equal to 0.05. So, this means that there are 5 chances in 100 (or 1 chance in 20) that the null hypothesis is correct, or to put it another way, there are 5 chances in 100 of being wrong by rejecting null hypotheses at this level. Investigators are never certain that the null hypothesis can be rejected, but they know that there is a 95% probability that they are correct in rejecting the null hypothesis. 

Discover the 5 different ways to detect multicollinearity.

Inferential Statistics Definition – The Limitations

When you are using inferential statistics, you need to understand not only the advantages of using it but you should also know its limitations. 

So, overall speaking, there are mainly two disadvantages or limitations of using inferential statistics. 

The first limitation and one that is present on all inferential statistics, is the fact that you are providing data about a population that you have not fully measured. So, you will not ever be able to completely understand that the values or statistics that you calculate are correct. After all, inferential statistics are based on the concept of using the values measured in a sample to estimate or infer the values that would be measured in a population. Ultimately, there is always a degree of uncertainty in doing this. 

The second limitation of inferential statistics is related to the first one. However, it is important to point out that some inferential tests require you to make educated guesses to run the inferential tests. So, as you can easily understand, there is also a bit of uncertainty in this process. And this may lead to repercussions on the certainty of the results of some inferential statistics.