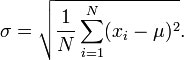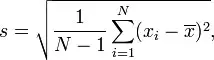When you are learning statistics, two of the first concepts that you will need to understand are the standard error of mean and the standard deviation. However, many students tend to confuse both. So, to prevent this from happening to you, we decided to tell you a bit more about each one of these concepts as well as show you the differences between them.
Discover the best statistic calculators online.
Standard Error Of Mean Vs Standard Deviation

Simply put, the standard deviation measures the amount of dispersion or variability for a specific set of data from the mean. On the other hand, the standard error of mean measures how far the sample mean of the data is likely to be from the true population mean.
One of the things that you should keep in mind is that the standard error of mean is always smaller than the standard deviation.
Check out our standard error calculator.
When They Are Both Used
Notice that in some instances, researchers can use both the standard error of mean and the standard deviation. This occurs, for example, in some clinical experimental studies.
In these particular cases, both the standard error of mean and the standard deviation are used to display the characteristics of the sample data as well as they both serve to explain the statistical analysis results.

Discover how to easily determine the standard error with our calculator.
A very important aspect to consider is that there are many researchers who tend to use both concepts as if they were the same. This is especially the case os studies related to medical literature. So, it is very important that these researchers keep in mind that the standard error of mean and the standard deviation are two different concepts. As we already explained above, the standard deviation is the dispersion of the data in a normal distribution. This simply means that this measure indicates how accurately the mean actually represents the sample data. On the other hand, the standard error of mean includes statistical inference that is based on the sampling distribution.
Calculating Standard Error Of Mean

As you can see, when you need to calculate the standard error of mean, you need to take the standard deviation and divide it by the square root of the sample size.
If you take a closer look at the standard deviation formula, then it is easy to understand that you need to follow some steps:
#1: Take the square of the difference between each data point and the sample mean, finding the sum of those values.
#2: Now, divide that sum by the sample size minus one, which is the variance.
#3: Finally, take the square root of the variance to get the SD.
Confirm your results with our simple standard error calculator.
Bottom Line
Simply put, the standard error of mean is just an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.
So, if the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.