Category : Variables

When you are looking at data statistics, there are many relevant concepts. And the reality is that one of the most important things that you need to realize is that the analysis needs to be appropriate for the scale of measurement of the variable. Notice that the focus of these decisions about scale needs to focus on levels of measurement that can be nominal, ordinal, ration, and interval.  

One of the things that you should keep in mind about these levels of measurement is the fact that they tell you about the amount of information in the variable itself. However, there are other ways to establish the difference between scales. 

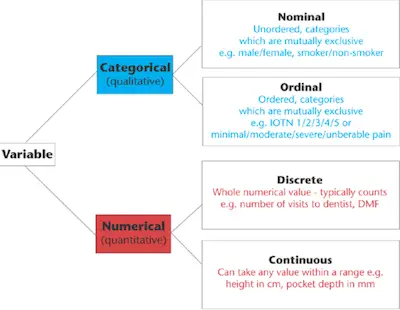
If you take a closer look at ratio-level variables, for example, you can find two different types: discrete and continuous. While discrete variables only take integers, continuous variables take on any value on a number line. In case you are wondering why this matters in statistics, the reality is that you measure the probabilities in a different way depending on if they are discrete or continuous distributions. 

The probability of each value of a discrete random variable is described through a probability distribution. At its simplest, this is a list of all the values in the set and the probability of each value occurring.

Discover how to calculate t value.

However, you need to know that the probabilities of many discrete random variables follow patterns that can be described with a mathematical function. This function is called a probability mass function.

As you can imagine, there are numerous discrete probability distributions including Bernoulli, binomial, hypergeometric, discrete uniform, and Poisson. There are explicit criteria that determine which probability distribution is appropriate for a specific discrete random variable.

Count data are a good example. A count variable is discrete because it consists of non-negative integers. Even so, there is not one specific probability distribution that fits all count data sets.

Looking for a t value calculator online?

The Poisson distribution often fits count data. It fits well when the mean of the variable is equal to its variance. So how do you determine that?

All you need to do is to run a summary of your variable in your statistical software package and then compare the mean to the variance. If the standard deviation is listed instead of the variance, just square the standard deviation. If they are almost equal, then that’s a good sign.

But many count variables fail these tests.

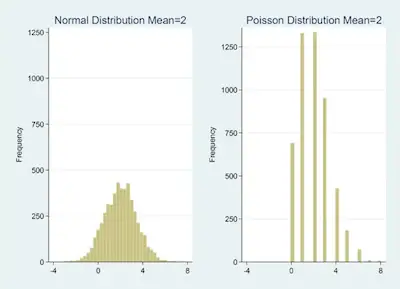
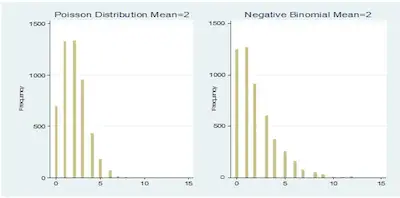
Below are two graphs generated with Poisson and negative binomial probability distribution functions. Each has 5,000 observations. The mean of the Poisson data is 2, the variance is 1.99, and the range is from 0 to 8. The mean of the negative binomial data is 2, the variance is 4.16, and the range is from 0 to 15.

The negative binomial distribution contains an extra parameter that allows the variance to be greater than the mean. If you tried to fit a data set with that mean and variance to a Poisson distribution, it would be considered overdispersed — not a good fit.

Check out our quick t student calculator.

The Normal Distribution

If the mean of a Poisson or negative binomial variable is high enough, it will be symmetric and bell-shaped. It will look like a normal distribution, except for one key distinction – normal variables are truly continuous, not discrete. This means that they can take on any possible value.

As a result, there are an infinite number of values (2.30546 is a different value than 2.30547). So, it makes no sense to calculate the probability that X is any exact value in a continuous variable. That probability is infinitesimal, a value approaching zero.

With continuous variables, the probability of a value falling within a range is calculated instead. For example, there is a 95% probability that a value from a normal distribution will fall within 1.96 standard deviations of the mean of that distribution.

To show you the difference, I created a set of 5,000 random values from a normal distribution with a mean and variance of 2. The range of the data is -2.512433 to 7.461702. Included next to its graph is the graph of the Poisson variable with a mean and variance of 2.

When you are looking at data sets, it is normal that you find some that have more than a thousand variables. So, while you may be compelled to continue with this complexity taking advantage of the speed of computers, you should stop right there. The reality is that, sometimes, when this occurs and you maintain all the dataset as it is, you end up with a vast array of poor results. So, how can you reduce the number of variables to analyze? 

Discover everything you need to know about statistics.

Why You Should Select Variables Before Analyzing The Data

One of the things that many students don’t realize is that working with a lot of data is a problem. After all, everything they can think of is on how to plunge into a data analysis and don’t even think about the step they are taking. However, this is something that should always be avoided. 

Whenever you have a new dataset, the first thing you need to do is to think about what you want to get from it. When you don’t take this step, you will probably end up with biased results. 

Looking for an online z calculator?

It is important that you are aware that there are many different and powerful techniques that you can use when dealing with many variables. One example is the multiple regression that allows you to include a very large number of predictor variables with the goal of maximizing the explanatory power of the model. But this isn’t the only one. You also have factor analysis, for example. However, and while it may nearly always produce a solution, it may well be a nonsense solution.

Ultimately, factor analysis is designed to identify sets of variables that are tapping the same underlying phenomenon. And it does this by examining the patterns of correlations among a set of variables.

Factor analysis is based on the assumption that the variables that are identified as belonging to a factor are really measuring the same thing. So, the factor itself is driving the responses on the individual variables. Therefore, they should not be causally related to each other.

Unfortunately, factor analysis cannot distinguish between variables that are causally related and those that are non-causally related. This can result in variables being grouped together when they should not be. 

Make sure to use our simple a value calculator.

How to Reduce the Number of Variables to Analyze

When you want to reduce the number of variables to analyze, you just need to think about the research question that you are trying to answer and to determine which data is directed. 

One of the ways that you have to do this is to simply draw diagrams of the model that you want to evaluate before you start analyzing the data. This way, you will need to first determine the dependent variable and only then the independent variable. In addition, you should also determine the likely mechanisms by which the independent and dependent variables might be related.

Check out our easy z stat calculator.

Notice that you should make some attempt to include variables that make sense together. In addition, you should avoid including variables where any correlation is more likely due to causal relationships than to the variables having something in common at the conceptual level.