Measurement Invariance And Multiple Group Analysis
When you are looking to create a quality scale for a variable that cannot be directly measured with one variable is not simple. In fact, it requires multiple steps. So, in these cases, you will need to use Structural Equation Modeling.
Notice that when creating scales is making sure the scale measures the latent construct equally well and the same way for different groups of individuals. Here’s a simple example: does your scale measure anxiety equally well for adults, adolescents, and children? Or does your scale measure assertiveness the same way for men and women?
Discover the best statistics calculators online.
When a scale measures a construct the same for different groups, this is called measurement invariance. However, it is important to keep in mind that you can’t just assume measurement invariance – you have to test it.
Testing For Measurement Invariance
When you are looking to test measurement invariance, you need to know that you can use 2 different methods: multiple group analysis and a simpler approach known as CFA with covariates. Today, we will only focus on the first one.
Multiple group analysis allows you to compare loadings, intercepts, and error terms in the groups’ measurement models. So, when you want to have a strong invariance, you need to show equal loadings of variables onto the latent variable and equal intercepts between groups.
Learn how cloud computing can benefit data science.
Here’s the comparison between groups:
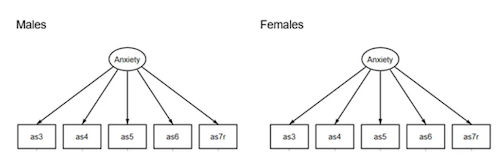
So, how can you determine the construct is measured consistently across groups?
As we mentioned above, you need to follow multiple steps:
Step #1: Rerun the Exploratory Factor Analysis (EFA) model separately for both groups.
In case you have different indicator variables load onto the constructs across groups, you can stop right there. The construct is inconsistent across groups. This is known as testing for dimensional invariance.
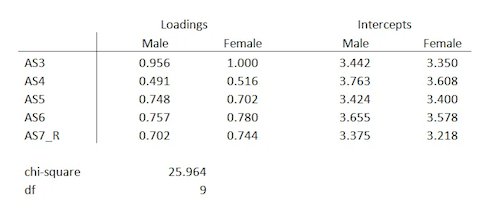
Step #2: Run a single model in which the two groups each have their own measurement model.
The indicators will be the same for each group, but you allow the software to estimate the loadings and intercepts uniquely for each group.
The loadings and intercepts will rarely be the same for both groups. But the question is, are they similar enough to be considered statistically the same?
Here are the estimated loadings and intercepts for the male and female measurement models (configural model):
Check out the 5 steps to take to collect high-quality data.
While they are not identical, you need to determine if they are close enough.
If you refit the model with the 2 groups but you force the factor loadings to be equal across groups, and allow the intercepts to be unequal – you are using the metric model.
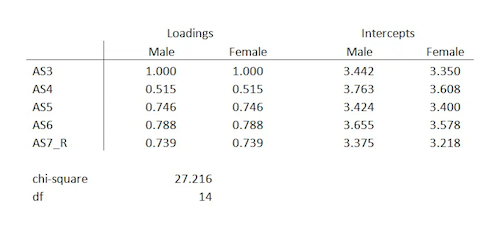
Now, you can already see that while the loadings between males and females are the same, the intercepts are still different.
Step #3: Fit the model with the factor loadings and intercepts equal across all groups (scalar model).
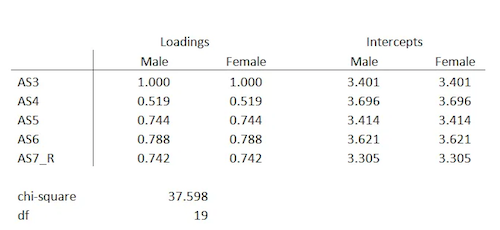
You should now take the difference between the metric and the scalar chi square model estimates again.
Understanding the F distribution.
In case the chi-square difference between the metric and scalar models is insignificant, we have group invariance. The change in chi-square above is 10.382, 5 degrees of freedom, p-value 0.065.
If you have group invariance, you know the construct is being measured the same across groups. You can then compare the differences between groups in a path analysis.