Factorial Design Basics For Statistics

When you are doing experiments with both physical and social sciences, one of the standards is that you use a random controlled experiment with just one dependent variable. However, there is a limitation to this design: it overlooks the effects that multiple variables can have with each other. 

When this occurs, you can use one of the most popular factorial design basics for statistics – the factorial design analysis of variance which is also known as the factorial ANOVA. 

Discover the best online statistics calculators.

A Simple Example

Let’s say that you just finished a college class in statistics and the final exam has gotten everyone talking about which majors do best – science or arts. At this moment, the class is mixed between art and science majors and underclassmen and upperclassmen. So, you decide to analyze the means of the final exam scores to figure out who is the best.

Learn more about confidence intervals.

The Main Idea Behind Factorial Design Basics For Statistics

If you remember the simple example we mentioned above, you have 2 variables that have an effect over the outcome: major and college experience, and each has two levels in it. So, this means that there are two independent variables and one dependent variable (final exam scores). 

Factorial design was born to handle this kind of design. Besides, the factorial ANOVA compares groups that may interact with one another. Instead of comparing two groups (majors and experience), you are actually comparing 4 groups:

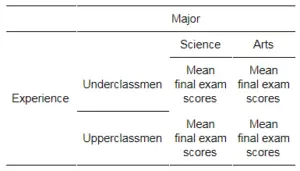
Here you have an example of 2 x 2 factorial design ANOVA. This means that there are two factors that we consider independent variables with two levels of treatment each. So, there will be four groups based on the combination of these factors.

Just like ANOVA, you will compare the means using the variances of each group and group level. However, you cannot simply do a series of ANOVAs because that would introduce too much error to confidently say there is a significant difference. So, you should only look for the main effects of each independent variable and how they potentially interact.

Discover how to interpret the F-test of overall significance in regression analysis.

Main Effects And Interactions

One of the best things about factorial analysis is the fact that it allows us to distinguish between main effects and potential interactions in the groups.

In one-way ANOVA, the main effect is present when the groups within a factor demonstrate a significant difference from the grand mean. In our example, the main effect would be a significant difference between upper and underclassmen or a difference between the arts and the sciences. 

An interaction is present when the dependent variable of the group is affected by a combination of both factors. In our example, a possible interaction would be between underclassmen status and being a science major. This would mean that there is a significant difference between this group and the others. 

Learn why adding values on a scale may lead to measurement error.

Looking At The Visual Differences

Getting back to our example, we will have two lines: the red one which represents the arts majors, and the blue one which represents the science majors.

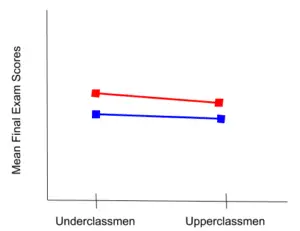
In the example above, you can see that the lines are close and almost parallel. This means that there is most likely no significant difference between majors, between college experience, and no interaction.

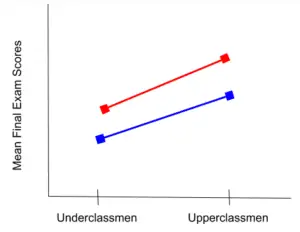
This example indicates that there is a main effect. We know this because, even though the lines are still approximately parallel, the mean final exam scores represent a difference. There is no interaction in this diagram.

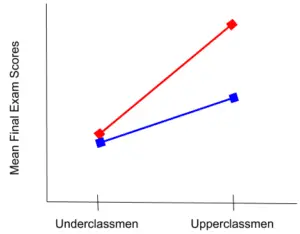
Now we have an example of an interaction. The lines are no longer parallel, so there is something going on between the two factors. This is an example of both a main effect and an interaction. You know there is a main effect because the mean final exam scores are different between under and upperclassmen. Since the lines cross (or would if we extend them) there is an interaction between major and college experience.