How To Calculate Standard Deviation Step By Step

Before we start by showing you how to calculate standard deviation, it is important to know exactly what the standard variation is.

What Is Standard Deviation In Statistics?

Simply put, the standard deviation in statistics is a measure of dispersion or variation between values in a specific set of data. It is usually represented by σ.

One of the thing that you need to understand is that the lower the standard deviation, the closer the data points will be to the mean or expected value, which is represented by μ. On the other hand, the higher the standard deviation, the wider is the range of the values.

The reality is that the standard deviation is used for many different things as we will see later on. Besides expressing population variability, the standard deviation is also used many times to determine the margin of error, for example. When you need to calculate standard deviation for this purpose, it is often referred to as standard error of the mean.

Find all the statistics calculators that you need.

Population Standard Deviation And Sample Standard Deviation

When we are talking about standard deviation, it is important to distinguish between population standard deviation and sample standard deviation.

• Population Standard Deviation:

This kind of standard deviation is used when an entire population can be measured. In this case, you need to use the following formula:

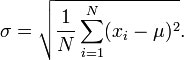
Where:

– xi is an individual value

– μ is the mean/expected value

– N is the total number of values

• Sample Standard Deviation

In some cases, it isn’t just possible to measure the entire population. So, you just can’t use the formula above.

When this happens, you will be forced to use a sample of the population that you need to study. While there are many different formulas to determine the sample standard deviation, we use the corrected sample standard deviation that is usually referred to as s.

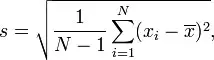
Where

– xi is one sample value

– x̄ is the sample mean

– N is the sample size

Why Do You Need To Calculate Standard Deviation?

While it is not normal that scientists calculate standard deviation manually since it can involve a lot of work and a lot of time, the truth is that it is important that you know how to do it as well as it is important that you understand what the standard deviation is used for.

The reality is that standard deviation is very used in industrial and experimental settings to test different models against real-world data. One of the areas that you know well and where standard deviation is very used is in product quality control. How?

You can use the standard deviation calculations to determine both a minimum and maximum value of a specific feature of a product. When it falls under or above, respectively, you will need to change it because it doesn’t have enough quality anymore.

However, standard deviation calculations can be used in other areas such as in weather. When you want to determine the differences in regional climate within the country, stand deviation can be quite helpful.

In case you like financials, then you surely will need to calculate standard deviation. After all, it can be very helpful when you need to determine the risk associated with the variations in the price of your asset or portfolio of assets.

There are many other situations that you can analyze by using the standard deviation. These are just some of them.

Calculate Standard Deviation Step By Step

Now that you understand the importance of standard deviation, let’s see how you can calculate it.

As we have already mentioned, this is something that is usually done by software. Nevertheless, we understand that it is important that you know how to calculate everything and each step that allows you to determine the standard deviation.

As you already know, standard deviation tells you how the numbers in your sample spread out.

Step #1: Find the mean, or average, of your sample.

Let’s say that you have the following data set: 10, 8, 10, 8, 8, and 4

The first thing you need to do before you calculate the mean of your sample is to look at the actual sample that you have. Take a deeper look at the numbers. Are they close to each other or they vary across a large range? What do this numbers represent? After all, you already know that you can use the standard deviation for multiple situations. So, the sample data that you have may refer to weight, height, test scores, heart rate readings, among so many others.

Now, it’s time to calculate the mean of your sample. Simply put, the mean is the average of all your points. Therefore, in order to calculate it, you’ll need to add all the numbers in your sample and then divide them by their total number.

So, according to our example, you have the following sample: 10, 8, 10, 8, 8, and 4

Mean = (10 + 8 + 10 + 8 + 8 + 4) / 6 = 48 / 6 = 8

Confirm your mean results here. 

Step #2: Subtract the mean from each number in the sample.

Now that you already determined the mean of your sample, you will now need to subtract this mean to each one of the numbers of your sample. So, you should end up with:

10 – 8 = 2

8 – 8 = 0

10 – 8 = 2

8 – 8 = 0

8 – 8 = 0

4 – 8 = -4

Step #3: Square all of the products from the previous step.

Since our main goal is to calculate the standard deviation, we need to make sure that we calculate the variance first.

In order to calculate the variance, you will need to square all the numbers that we just found in the previous step. So, this is how you should end up:

2^2 = 4

0^2 = 0

2^2 = 4

0^2 = 0

0^2 = 0

(-4)^2 = 16

Step #4: Add the squared products together.

All that you need to do in this step is to sum up all the values that you calculated in the previous step. So, you’ll end up with:

4 + 0 + 4 + 0 + 0 + 16 = 24

So, your sum of squares is 24.

Step #5: Divide the sum of the squared products by (n-1)

In this step, you will need to divide the sum of the squared products by (n-1). In case you don’t know, n is the number of total numbers that you have in your sample. In our example, we had already determined that we have 6. So, n = 6, where (n-1) = 5.

You also already know that your sum of squares that was determined in the previous step is 24.

So, the variance of your sample is:

Variance = 24 / 5 = 4.8

Step #6: Calculate the square root of the variance to find the standard deviation.

Finally, it’s time to determine the standard variation of your sample.

In order to do it, you just need to use the variance that you determined previously and take the square root of it.

As you still remember, we determined that the variance of our sample was 4.8.

So, in order to determine the standard deviation:

Standard Deviation = √4.8 = 2.19