Should Confidence Intervals or Tests of Significance be Used?
When you are learning statistics, it is normal that you learn about confidence intervals. But what are confidence intervals?
What Are Confidence Intervals?
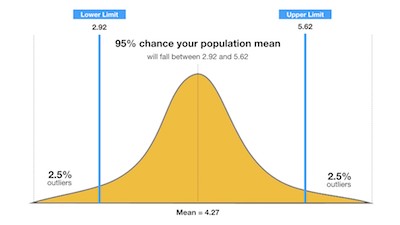
When you use a sample of the population, you are subject to sampling error. After all, as you can easily understand, sample statistics can’t match exactly the population parameters that they estimate.
Discover the best statistics calculators online.
Therefore, you need to think that you may have a sampling error.
One of the things that you can do to deal with sampling error is to simply ignore results if you believe there is a chance that they could be due to sampling error. In case you don’t know, this is the approach that you should use when you are working with significance tests. As a rule of thumb, sample effects are treated as being zero when you have more than 5% or 1% chance they were produced by sampling error.
Check out our confidence interval calculator for the population mean.
However, instead of using significance tests, you may prefer using confidence intervals. In this case, instead of deciding whether a sample data support that the null hypothesis is true, you can, instead, take a range of values of a sample statistic that is likely to contain a population parameter. In this case, a certain percentage of intervals that is referred to as the confidence level will include the population parameter in the long run (over repeated sampling).
The Interpretation
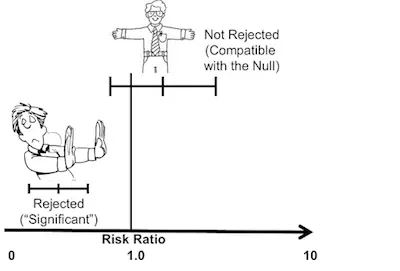
When you are using confidence intervals, then you need to understand that for any given sample size, the wider the confidence interval, the higher the confidence level. On the other hand, a narrower confidence interval or a more precise one needs to use either a lower level of confidence or a larger sample.
Learn more about the different methods and types of sampling.
Let’s imagine that you have a sample that tells you that 52% of the participants stat they intend to vote for Party Y at the next election. As you can easily see, this figure is merely a sample estimate.
The reality is that since this percentage came from a sample that has sampling error, then you need to allow a margin of error. So, when you use confidence interval, you can better estimate the interval within which the population parameter is likely to lie.
As you can easily see, using confidence intervals prevents you from dealing with the confusing logic of null hypothesis testing and its simplistic significant/not significant dichotomy.
If you think about it, confidence intervals are actually a form of inferential analysis and they can be used with many descriptive statistics. These include percentages, correlation coefficients, regression coefficients, and percentage differences between groups.
Just like tests of significance, confidence intervals always assume that the sample estimate comes from a simple random sample. So, you won’t be able to use them on data from non-probability samples.
Discover how to find a confidence interval.
Why It Is Better To Use Confidence Intervals Than Significance Tests
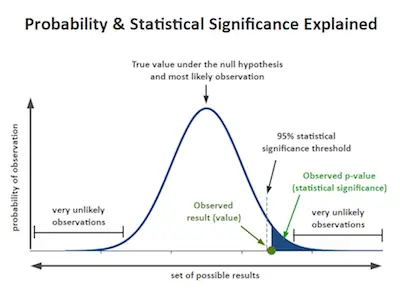
- Confidence intervals provide all the information that a test of statistical significance provides and more. If at the 95 percent confidence level, a confidence interval for an effect includes 0 then the test of significance would also indicate that the sample estimate was not significantly different from 0 at the 5 percent level.
- The confidence interval provides a sense of the size of any effect. The figures in a confidence interval are expressed in the descriptive statistic to which they apply (percentage, correlation, regression, etc.).
- Since confidence intervals avoid the term ‘significance’, they avoid the misleading interpretation of that word as ‘important.’ Confidence intervals remind us that any estimates are subject to error and that we can provide no estimate with absolute precision.