The Difference Between Association and Correlation
One of the questions many statistics students have is to know the difference between association and correlation. The truth is that many believe that association and correlation are the same thing or mean the same thing. However, and even though this may sound a silly question, the truth is that both concepts can make arise the similarity or difference between the two concepts.
Understanding statistics in 2020.
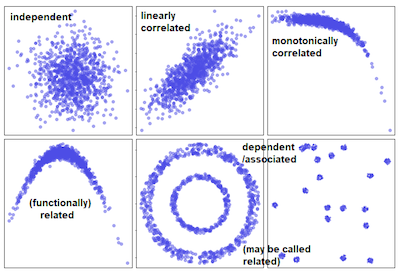
The reality is that this confusion can be understood because in regular English, correlated and associated at both related to the same thing. On the other hand, in technical terms, correlation is the strength of association as measured by a correlation coefficient. In what concerns to
association, this is not a technical term at all. It simply means the presence of a relationship: certain values of one variable tend to co-occur with certain values of the other variable.
Looking for a standard error calculator?
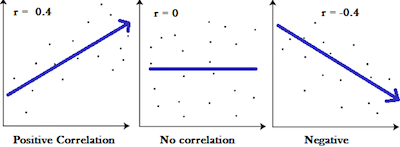
One of the things that you need to keep in mind is that correlation coefficients vary between -1 and 1. When they are equal to -1, this means that there is a perfect negative relationship: high values of one variable are associated with low values of the other. Likewise, a correlation of +1 describes a perfect positive relationship: high values of one variable are associated with high values of the other. When the correlation coefficients are equal to zero, this means that there is no relationship. The same is saying that high values of one variable co-occur as often with high and low values of the other. There is no independent and no dependent variable in a correlation. It’s a bivariate descriptive statistic.
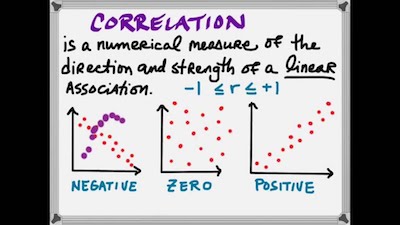
The most common correlation coefficient is the Pearson correlation coefficient. Often denoted by r, it measures the strength of a linear relationship in a sample on a standardized scale from -1 to 1.
It is so common that it is often used synonymously with correlation.
Check out our standard error online calculator.
Notice that Pearson’s coefficient assumes that both variables are normally distributed. This requires they be truly continuous and unbounded.
But when you’re interested in relationships of non-normally distributed variables, you should use other correlation coefficients that don’t require the normality of the variables. Some include the Spearman rank correlation, point-biserial correlation, rank-biserial correlation, tetrachoric, and polychoric correlation.
Notice that there are still other measures of association that don’t have those exact same properties. They tend to be often used where one or both of the variables is either ordinal or nominal. These tend to include measures such as phi, gamma, Kendall’s tau-b, Stuart’s tau-c, Somer’s D, and Cramer’s V, among others.
Here’s how to calculate standard error online.
Bottom Line
The most important thing that you need to keep in mind is that there is a difference between association and correlation. Besides, you also need to be aware that there are many different measures of association. However, only some of these are correlations.
Notice that while we are clearly establishing a difference between association and correlation, there isn’t really a consensus between researchers and analysts in this matter. So, you should always clearly explain what you mean with both association and correlation to avoid any misinterpretations.