Understanding The Mean And Median

There’s no question that the mean and median are two different measures that are widely used in statistics. After all, they are very effective when you want to describe the most typical value in a set of values. Notice that both mean and median are measures of central tendency. 

Use the best online statistics calculators.

The Mean And Median

As you can imagine, the mean and the median are two different concepts. And we believe that the best way to understand them is by showing an example. 

Let’s say that you draw a sample of 5 teenage boys and you measure their weights. You discover that they weight100 pounds, 100 pounds, 130 pounds, 140 pounds, and 150 pounds.

Now, you are asked to calculate both the mean and median. 

To calculate the mean of the sample, you will need to add all the observations and then divide them by the number of observations. So, in this specific example:

Mean = 100 + 100 + 130 + 140 + 150) / 5 

Mean = 620/5

Mean = 124 pounds

Click here to calculate the mean.

To calculate the median, you will need to arrange your data in order from the smallest to the largest value. You will then need to see if your sample size id odd or even. In case you have an odd number of observations, then the median is just the middle value. On the other hand, if you have an even number of observations, then the median is the average of the two middle values. So, in this specific example:

100 100 130 140 150

Since we have an odd number of observations (5), then the median is the middle value, 130 pounds. 

Click here to calculate the median.

Mean Vs Median

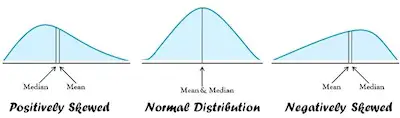
One of the things that many students wonder is about the importance of each one of these measures of central tendency. However, it’s important to look at both the mean and median as measures that have advantages and disadvantages and not in terms of importance. 

The median, for example, can be a better indicator of the most typical value if a set of scores has an extreme value that differs greatly from other values. On the other hand, it is also important to notice that when you have a very large sample size that doesn’t include these extreme values, then the mean is a better measure of central tendency. 

Check out our mean, media, mode, range calculator. 

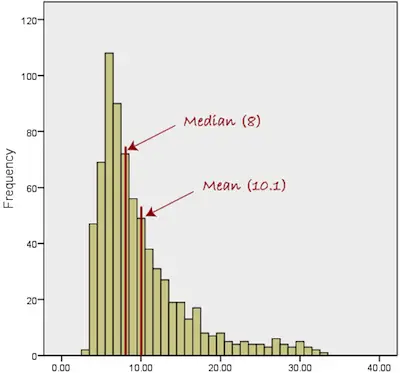
But here’s a simple example so that you can fully understand these concepts and their advantages and disadvantages. 

Let’s say that you are looking at a sample of 10 households to estimate the family’s income. According to the data you collected, nine of the households have incomes between $20,000 and $100,000 but the tenth household has an annual income of $1,000,000,000. 

As you can see, the tenth household is an extreme value. So, if you want to use a measure of central tendency, then you should consider using the median. After all, if you use the mean instead, you will get an over-estimated value because of this tenth household. 

Bottom Line

As you can see, both the mean and median are important when you are analyzing data. However, using one or the other may be better depending on the samples that you need to analyze.