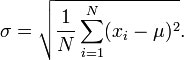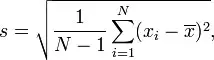Category : Blog

All You Need To Know About The ANOVA F Value

Simply put, the ANOVA (or analysis of variance) can help you determine if the means of 3 or more groups are different. In order to do this, ANOVA uses the F tests to test if the means are equal or not.

Before we start with the ANOVA F value explanation, we need to ensure that you know everything that you need about the F statistic. The F statistic is simply the ratio of two variances. As you already know, variances are a mean of dispersion. So, this means that variances measure how far the data are scattered from the mean. Ultimately, the larger the values, the larger the dispersion you will have.

Use the statistic tables you need.

anova-f-value

One of the things that you need to know about F tests is that they are very helpful and flexible. After all, you can use them in a wide variety of situations. You can use the F tests and the F statistics not only to test the equality of means but also to test specific regression terms, to compare the fits of different models, and even to test the overall significance for a regression model.

Why Using ANOVA F Value And Not A T Test?

When you have a lot of data, making a t test can be virtually impossible because they won’t provide you with accurate results. Just imagine that you want to make a t test for 4 different groups. So, you will end up with 8 pairwise comparisons. You need to compare group 1 with groups 2, 3, and 4. Then, you need to compare group 2 with groups 4 and 5, and so on. Even though you may think you have a 5% probability of a type I error, the truth is that you need to consider that you are dealing with 8 different pairwise comparisons. So, you just can’t expect them all to be significant.

If you need to calculate the t-statistic, use our T-Statistics and degrees of freedom calculator. 

 

So, what can you do? The best chance that you have is to use the ANOVA F value.

Let’s imagine that you want to compare the heights of different children who have adopted a regular dit and other children who have adopted a vegan diet. So, now that the children are 13 years all, you decide to measure their heights.

The first thing that you need to think about is on the null hypothesis. With the ANOVA F value, the null hypothesis is that the means are all the same. So, μ1 = μ2 = μ3.

Learn how to calculate the standard deviation.

Now, it’s time to do the F test. In statistics, the F statistic formula is the following one:

F Statistics = variance between groups / variance within groups

In the case that it is proved that the null hypothesis is correct, these two variances should be very similar and you should end up with an F statistic value near 1.

Calculating Variance Within Groups

One of the questions that many people have is related to the way that you have to calculate the variance within groups. If this is also your case, the formula is very straightforward:

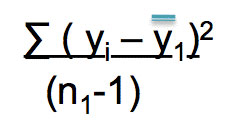
within-group-variance-formula

This calculation should be done for each one of the groups individually. However, you need to consider that not all groups are created the same way. So, you will need to weight these group variances using the degrees of freedom for each group. As you know, the degrees of freedom are equal to the total of the sample data minus 1.

So, you should get to a formula like the following one:

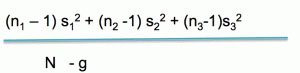
within-group-variance-weightened

Calculating Variance Between Groups

In order to calculate the variance between groups, you need to use the following formula:

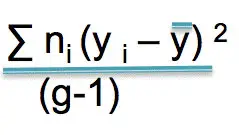
Variance-Between-Groups-formula

Here are the steps that you need to take:

#1:  Subtract the mean of each group by the overall mean and square the result.

#2: Multiply the result you got by the number in each group.

#3: Add the result.

#4: Divide the result by the number of groups that you have minus 1.

7-30-2018 | Comments Off on All You Need To Know About The ANOVA F Value

F Test Example – A More Practical Insight

If you are studying statistics at school, you probably already heard about the F test. But what is the F test exactly?

Simply put, the F test is a general name that is given to all the tests that need to use the F-distribution. So, when you hear someone talking about the F test, they are probably referring to the F test that serves to compare two variances. Nevertheless, the F test can be used in a wide variety of tests.

Check the best online stat tables. 

f-test-example

While you may have some questions about the F test and how to determine its value, we believe that before we show you an f test example, we should define the F test better.

When Should You Use An F Test?

There are two different occasions on which you should an F test. These include:

– When you need to compare the variability of a new method versus an old method

– When you want to compare the two different variances that you got when you used a t test.

F Test Assumptions

There are a couple of assumptions that you need to know about when you want to perform an F test. The truth is that in order to perform this kind of test, you need to ensure that the population is approximately normally distributed.

 

F-test-normal-distribution

In addition, you also need to ensure that the samples are independent events. Besides all this, you also need to bear in mind that:

– In case you are given standard deviations to make the calculations, you need to square them in order to get the variances,

– The larger variance should always be in the numerator so that the result is a positive one. This ensures that the calculations are easier to make.

– In case the degrees of freedom you need aren’t listed in the F table, you should use the critical value that is larger to avoid any errors.

– In case you are performing two-tailed tests, you need to ensure that you divide alpha by 2 before you calculate the right critical value.

F Test Example:

Now that you already know the assumptions and the factors that you need to keep in mind when you need to do an f test, it’s time to show you a practical f test example.

In this F test example, we will be comparing two variances by hand.

Step #1: If you were given standard deviations, you need to ensure that you square them to get the respective variances.

So, let’s say that you have the following standard deviations:

σ1 = 9.6

σ2 = 10.9

 

F-critical-value

In order to know the variances (s1 and s2), you will need to:

s1 = 9.6^2 = 92.16

s2 = 10.9^2 = 118.81

Use our critical F value calculator to confirm your results.

Step #2: Now, it’s time to divide the variances to get the F value. As we already told you, you need to use the higher variance number on the numerator and divide it by the smallest variance.

So, supposing that you have:

s1 = 2.5

s2 = 9.4

F = s2 / s1 = 9.4 / 2.5 = 3.76

Step #3: In this step, you will find the degrees of freedom. In case you don’t know, the degrees of freedom is equal to the size of your sample minus 1. Since we have two samples (variance 1 and variance 2), this means that you have two degrees of freedom – one for the numerator and the other one for the denominator.

Take a look at our Confidence Interval Calculator for the Population Mean.

Step #4: It’s now time to take a look at the F table and look for the F value that you calculated.

Step #5: Finally, it’s time to withdraw conclusions from our F test example. In this step, you will need to compare the value that you calculated on step 2 ( F = 3.76 ) with the table F value that you discovered in the previous step.

If the table F value is smaller than the value you calculated, then you can say that you reject the null hypothesis.

| Comments Off on F Test Example – A More Practical Insight

A Reliable Tool For Chi Square Test Online

One of the best statistical tests that you can perform when you want to discover how likely it is to have the observed data fit what you expect is the chi square test online. After all, the chi square test online is simple and effective and allows you to analyze categorical data (data that can be divided into categories).

chi-square-test-online

Take a look at the best statistics calculators.

One of the things that you need to understand about the chi square test online is that it isn’t suited to work with continuous data or percentages.

The Chi Square Test And The Null Hypothesis

One of the things that you need to know when you are making a chi square test is that the null hypothesis always assumes that the variables are independent which is the same as saying that the observed data doesn’t fit the model.

Chi Square Formula And Its Application

In order to make a chi square test, you need to use its formula. The truth is that it is a fairly simple and intuitive formula:

chi-square-formula

As you can see, you shouldn’t have any problems using it. However, when you have a lot of data, this process can be very tedious. So, we decided to show you a simple example with only a small set of data so that you can easily understand what you need to do to calculate the chi square value.

Let’s say that we want to know more about the relationship between the party affiliations and how they are distributed between males and females.

So, just take into consideration:

The Observed Data

DemocratRepublicanTotal
Male203050
Female302050
Total5050100

 

The Expected Data

DemocratRepublicanTotal
Male252550
Female252550
Total5050100

 

So, by using the formula we displayed above, you just need to replace the data that we have on the tables for the respective variables.

X^2 = ((20-25)^2/25) + ((30-25)^2/25) + ((30-25)^2/25) + ((20-25)^2/25)

X^2 = (25/25) + (25/25) + (25/25) + (25/25)

X^2 = 1 + 1 + 1 + 1 = 4

Confirm your results with our chi square value calculator. 

So, you just discovered that the chi square is 4. But what does this mean? What can you conclude?

The truth is that simply looking at the chi square value you can’t conclude much. This is why you need to use the chi square test online which will help you achieve a much more interesting value – the p-value.

In order to calculate the p-value, you need to know the chi square value but you also need to know the degrees of freedom.

The Degrees Of Freedom

chi-square-value---using-excel

Usually denoted as d or df, the degrees of freedom are able to tell you how many numbers in your table are independent. The degrees of freedom are very important when you are performing a chi square test. After all, they factor the probability of independence into your calculations.

Discover how to find the Z score. 

So, after you have the chi square value, you need to take a look at the chart. The degrees of freedom will be expressed on the left. All you need to do is to check the row that has the closest number to the chi square value you got, and then just see the respective number located in the top row. This will give you the “Significance Level” or approximate probability for that value.

Returning to our example, we got a chi square value and a degree of freedom of 1. So, by looking at the table, we can see that we have a p-value of 0.0455. This value means that there is a 4.6% probability of the null hypothesis to be correct.

| Comments Off on A Reliable Tool For Chi Square Test Online

What Does Range Mean In Math?

The range is one of the terms that is used very often in math. Besides, it is also one of the easiest ones to understand.

Simply put, the range is only the difference between the highest value and the lowest value within any set of numbers.

Let’s say that you have the following set of numbers:

34 47 45 42 37 35 40

In order to determine the range, the only thing you need to do is to determine the difference between the highest number of the set to the lowest number of the set.

So, the range in this case is:

Range = 47 – 34 = 13

Take a look at the best statistics calculators.

While the range seems pretty obvious and easy to calculate, please notice that the set of numbers we gave as an example are very close to each other.

So, let’s now assume that you have a different set of numbers for which you need to discover the range:

8, 11, 5, 9, 7, 6, 3616

As you can see, the highest value in this set is 3616 and the lowest value in this same set is 5. Even though according to the rules, you would need to find the difference between these two numbers to determine the range, you wouldn’t get a precise range. After all, all the numbers in the set with the exception of the 3616 are all near 10. So, having a range of 3611 (3616 – 5) doesn’t really make a lot of sense.

So, what can you do?

Whenever you have a specific set of numbers that either has extremely low values or extremely high values, you should prefer to use the standard deviation.

How Can You Use The Standard Deviation?

When you have a set of numbers that include extremely high values or extremely low values, you should calculate the standard deviation instead of the range.

Here is how you can easily do it.

Let’s say that you have the following set of values: 3 9 6 10 145

As you can see, the 145 is an extremely high value compared to al the others. So, in this case, you need to calculate the standard deviation instead of the range.

1. Determine the mean of the set of values:

In order to determine the mean, you will need to add them all and then divide the result by the total number of values that are included in the set.

According to our example, we have 5 values. So:

Mean = (3 + 6 + 9 + 10 + 145) / 5 = 34.6

You can also use our Range calculator to help you with your calculations. 

2. You will now need to subtract each number from the mean:

According to our example, you will need to do the folowing calculations:

3 – 34.6 = – 31.6

6 – 34.6 = -28.6

9 – 34.6 = -25.6

10 – 34.6 = -24.6

145 – 34.6 = 110.4

3. You will now need to find the squared result for each one of the numbers you got:

(-31.6)^2 = 998.56

(-28.6)^2 = 817.96

(-25.6)^2 = 655.36

(-24.6)^2 = 605.16

110.4^2 = 12188.16

Summing up all the squares: 15265.2

Now, you need to divide the sum of all squares by (n-1):

15265.2 / (5 – 1) = 3816.3

So, you just have the variation of your set of numbers: 3816.3.

When you just need to make simple calculations, make sure to use our free calculator. 

4. Finally, calculate the standard deviation:

In order to calculate the standard deviation, you just need to take the square root of the variance:

Standard Deviation = √3816.3 = 61.776

As you can see, this number makes a lot more sense than simply determining the range.

5-31-2018 | Comments Off on What Does Range Mean In Math?

How To Find Z Score For A Normally Distributed Data

The z score, that is also known as the standard score, is a very useful statistic. After all, it allows you to determine the probability of a score that is occurring within your normal distribution, as well as it also allows you to compare two scores that have different normal distributions.

When you want to know how to find z score, you will discover that it will convert, or standardize, scores in a normal distribution to z scores. So, it will become a standard normal distribution.

How To Find Z Score?

While we could go on with a theoretical explanation, we believe that it will be a lot easier for you to understand how to find z score if we use an example.

Make sure that you check out our stat tables. 

Let’s say that your Math teacher decided to do a test and that your class has 50 students. According to his findings, your teacher saw that the mean score was 60 out of 100 and that the variation in scores, or the standard variation, was 15 marks.

So, at this point, you took a look at your test result and you asked your teacher if you had done well by scoring 70 out of 100.

At first sight, it seems that you have done well. After all, considering that the mean score was 60 and you were able to score 70, apparently you did well. However, this conclusion doesn’t include the variations in the scores of all the students in your class. Putting it into statistical terms, it doesn’t consider the standard deviation.

So, how can you know if you did well?

The Standard Normal Distribution And The Standard Score (Z Score)

Whenever you are taking into consideration a normally distributed data, in order to discover the z score you will need to standardize the results.

One of the things that you need to understand is that the standard normal distribution only converts the group of data in your frequency distribution. In order to do it, it considers that the mean is zero and that the standard deviation is 1, just as it is shown in the following chart:

how-to-find-z-score

Since a z score is expressed in terms of the standard deviation from its means, we can use the following formula to determine it:

z-formula

where:

– X = score

– µ = mean

– σ = standard deviation

In case you want to confirm your results, just use our Z Score Calculator.

So, returning to our example, how can you know if you did well or not?

The truth is that in order to discover it, you can rephrase the question: What number (or percentage) of students scored higher than you and what number (or percentage) of students scored lower than you?

If you remember our example, you were able to score 70 out of 100, and the mean score was 60. In addition, we also know that the standard deviation was 15.

So, if you use the z score formula and replace the values for the variables, you will get:

Standard Score,z = ( X – µ ) / σ = (70 – 60) /15 = 10 / 15 = 0.6667

So, you now know that your z score is 0.67. However, since you need to work with either the number or the percentage of students, you need to use a z score table.

normal-distributions

As you can see in the table shown, you’ll need to find 0.6 in the y-axis, and the 0.07 in the x-axis. In this case, you will see a value of 0.2514.

But what does this number mean? Simply put, it means that the probability of a score is greater than 0.67 is 0.2514. If we multiply it by 100 to get the percentage, we can say that about 25% of the students in your class got a better mark than you.

So, while it seemed that you had done well on the test, we can say that you did better than most other students in your class, you weren’t one of the best.

| Comments Off on How To Find Z Score For A Normally Distributed Data

How To Calculate Standard Deviation Step By Step

Before we start by showing you how to calculate standard deviation, it is important to know exactly what the standard variation is.

What Is Standard Deviation In Statistics?

Simply put, the standard deviation in statistics is a measure of dispersion or variation between values in a specific set of data. It is usually represented by σ.

One of the thing that you need to understand is that the lower the standard deviation, the closer the data points will be to the mean or expected value, which is represented by μ. On the other hand, the higher the standard deviation, the wider is the range of the values.

The reality is that the standard deviation is used for many different things as we will see later on. Besides expressing population variability, the standard deviation is also used many times to determine the margin of error, for example. When you need to calculate standard deviation for this purpose, it is often referred to as standard error of the mean.

Find all the statistics calculators that you need.

Population Standard Deviation And Sample Standard Deviation

When we are talking about standard deviation, it is important to distinguish between population standard deviation and sample standard deviation.

  • Population Standard Deviation:

This kind of standard deviation is used when an entire population can be measured. In this case, you need to use the following formula:

calculate-standard-deviation

Where:

– xi is an individual value

– μ is the mean/expected value

– N is the total number of values

  • Sample Standard Deviation

In some cases, it isn’t just possible to measure the entire population. So, you just can’t use the formula above.

When this happens, you will be forced to use a sample of the population that you need to study. While there are many different formulas to determine the sample standard deviation, we use the corrected sample standard deviation that is usually referred to as s.

sample-standard-deviation-formula

Where

– xi is one sample value

– x̄ is the sample mean

– N is the sample size

Why Do You Need To Calculate Standard Deviation?

While it is not normal that scientists calculate standard deviation manually since it can involve a lot of work and a lot of time, the truth is that it is important that you know how to do it as well as it is important that you understand what the standard deviation is used for.

The reality is that standard deviation is very used in industrial and experimental settings to test different models against real-world data. One of the areas that you know well and where standard deviation is very used is in product quality control. How?

You can use the standard deviation calculations to determine both a minimum and maximum value of a specific feature of a product. When it falls under or above, respectively, you will need to change it because it doesn’t have enough quality anymore.

However, standard deviation calculations can be used in other areas such as in weather. When you want to determine the differences in regional climate within the country, stand deviation can be quite helpful.

In case you like financials, then you surely will need to calculate standard deviation. After all, it can be very helpful when you need to determine the risk associated with the variations in the price of your asset or portfolio of assets.

There are many other situations that you can analyze by using the standard deviation. These are just some of them.

Calculate Standard Deviation Step By Step

Now that you understand the importance of standard deviation, let’s see how you can calculate it.

As we have already mentioned, this is something that is usually done by software. Nevertheless, we understand that it is important that you know how to calculate everything and each step that allows you to determine the standard deviation.

As you already know, standard deviation tells you how the numbers in your sample spread out.

standard-deviation-chart

Step #1: Find the mean, or average, of your sample.

Let’s say that you have the following data set: 10, 8, 10, 8, 8, and 4

The first thing you need to do before you calculate the mean of your sample is to look at the actual sample that you have. Take a deeper look at the numbers. Are they close to each other or they vary across a large range? What do this numbers represent? After all, you already know that you can use the standard deviation for multiple situations. So, the sample data that you have may refer to weight, height, test scores, heart rate readings, among so many others.

Now, it’s time to calculate the mean of your sample. Simply put, the mean is the average of all your points. Therefore, in order to calculate it, you’ll need to add all the numbers in your sample and then divide them by their total number.

So, according to our example, you have the following sample: 10, 8, 10, 8, 8, and 4

Mean = (10 + 8 + 10 + 8 + 8 + 4) / 6 = 48 / 6 = 8

Confirm your mean results here. 

Step #2: Subtract the mean from each number in the sample.

Now that you already determined the mean of your sample, you will now need to subtract this mean to each one of the numbers of your sample. So, you should end up with:

10 – 8 = 2

8 – 8 = 0

10 – 8 = 2

8 – 8 = 0

8 – 8 = 0

4 – 8 = -4

Step #3: Square all of the products from the previous step.

Since our main goal is to calculate the standard deviation, we need to make sure that we calculate the variance first.

In order to calculate the variance, you will need to square all the numbers that we just found in the previous step. So, this is how you should end up:

2^2 = 4

0^2 = 0

2^2 = 4

0^2 = 0

0^2 = 0

(-4)^2 = 16

Step #4: Add the squared products together.

All that you need to do in this step is to sum up all the values that you calculated in the previous step. So, you’ll end up with:

4 + 0 + 4 + 0 + 0 + 16 = 24

So, your sum of squares is 24.

Step #5: Divide the sum of the squared products by (n-1)

In this step, you will need to divide the sum of the squared products by (n-1). In case you don’t know, n is the number of total numbers that you have in your sample. In our example, we had already determined that we have 6. So, n = 6, where (n-1) = 5.

You also already know that your sum of squares that was determined in the previous step is 24.

So, the variance of your sample is:

Variance = 24 / 5 = 4.8

Step #6: Calculate the square root of the variance to find the standard deviation.

Finally, it’s time to determine the standard variation of your sample.

In order to do it, you just need to use the variance that you determined previously and take the square root of it.

As you still remember, we determined that the variance of our sample was 4.8.

So, in order to determine the standard deviation:

Standard Deviation = √4.8 = 2.19

| Comments Off on How To Calculate Standard Deviation Step By Step

« Previous Page