How To Use Descriptive Analysis In Research
Before we get into how to use descriptive analysis in research, we believe that it is important to define what descriptive analysis is in the first place.
What Is Descriptive Analysis?
Simply put, descriptive analysis is one of the two main types of statistical analysis and it can be defined as the brief descriptive coefficients that summarize a specific data set which can be either a representation of the entire or a sample of a population.

Learn everything you need to know about statistics.
One of the things that you should keep in mind about descriptive analysis is that it can be broken down into measures of central tendency and measures of variability (spread). In case you don’t remember, the measures of central tendency include the mean, median, and mode, while the measures of variability include the standard deviation, variance, the minimum and maximum variables, and the kurtosis and skewness.
Understanding Descriptive Analysis

Overall, descriptive analysis helps describe and understand the features of a specific data set giving short summaries about the sample and measures of the data.
As we already mentioned above, the most known or recognized types of descriptive statistics are measures of center: the mean, median, and mode, which are used at almost all levels of math and statistics.
The mean which is the average is calculated by adding all the figures within the data set and then dividing by the number of figures within the set.
Let’s say that you have the following data set: 2, 3, 4, 5, 6.
So, the mean is 4 ((2 + 3 + 4 + 5 + 6)/5).
The mode of the data set is the value that appears more often. And the median is the value that appears in the middle of the data set when the values are ordered from the smallest to the largest.
Discover how you should use the student’s t test.
One of the most interesting facts about descriptive analysis is that it is mainly used to repurpose hard-to-understand quantitative insights across a large data set into bite-sized descriptions.
Let’s take the GPA (grade point average) as an example. Simply put, this provides a good understanding of descriptive statistics. After all, the idea of a GPA is that it takes data points from a wide range of grades, classes, exams, and averages them together to provide a better understanding of a student’s overall academic capabilities. So, ultimately, a student’s personal GPA simply refers to the student’s mean academic performance.
These are the degrees of freedom for t tests.
Measures Of Descriptive Analysis In Research
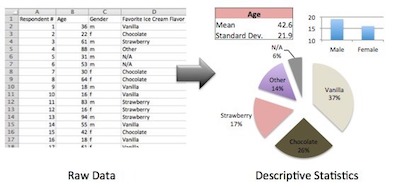
As we already mentioned, descriptive statistics are either measures of central tendency or measures of variability which are also known as measures of dispersion.
While the measures of central tendency focus on the average or middle values of data sets, the measures of variability focus on the dispersion of data. These two measures use graphs, tables, and general discussions to help people understand the meaning of the analyzed data.
Measures of central tendency describe the center position of a distribution for a data set. A person analyzes the frequency of each data point in the distribution and describes it using the mean, median, or mode, which measures the most common patterns of the analyzed data set.
Take a look at the advantages and disadvantages of measures of central tendency.
In what concerns the measures of variability, they aid in analyzing how spread-out the distribution is for a set of data. For example, while the measures of central tendency may give a person the average of a data set, it does not describe how the data is distributed within the set. So, while the average of the data may be 65 out of 100, there can still be data points at both 1 and 100. Measures of variability help communicate this by describing the shape and spread of the data set. Range, quartiles, absolute deviation, and variance are all examples of measures of variability.